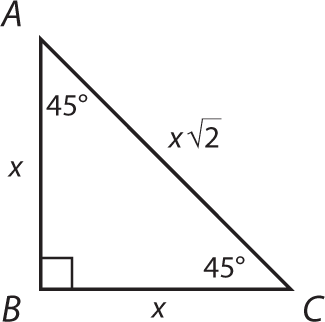Home Posts Categories Tags

GMAT Quant Notes

 included in  category Cognition and Learning
     1225 words   6 minutes 

I’m not planning on taking the GMAT any time soon, but was curious to see what would be involved anyway. These notes are far from exhaustive - they’re just a few things that I want to remind myself of.

Book: GMAT All the Quant by Manhattan Prep.

A. Statement (1) does allow you to answer the question, but statement (2) does not.

B. Statement (2) does allow you to answer the question, but statement (1) does not.

C. Neither statement works on its own, but you can use them together to answer the question.

[C is often a trap answer]

D. Statement (1) works by itself and statement (2) works by itself.

E. Nothing works. Even if you use both statements together, you still can’t answer the question.

Whether you use AD/BCE or BD/ACE, you will always:

  • Cross off the top row if the first statement you try is not sufficient
  • Cross off the bottom row if the first statement you try is sufficient

Sufficiency from testing:

  • 1+ yes and 1+ no = sufficient
  • Sometimes =/= insufficient

\[\frac{45}{76}>\frac{65}{87}?\]

\[45\times87=3915\\76\times65=4940\\3915>4940\]

Therefore the statement is correct.

Also:

\[76 \times 87 = 6612\]

So:

\[\frac{45}{76}±\frac{65}{87}=\frac{3915±4940}{6612}\]

70% = 50% + 10% + 10%

18% of 50 = 50% of 18

876.3 × 43.5464 → total 5 decimal places → 8763 × 435464 = 3815971032 → 38159.71032

876.3 / 43.5464 → max 4 decimal places so × both by 10000 → 8763000 / 435464 = 20.123

When simplifying an expression: BODMAS

When simplifying an equation: reverse BODMAS

Good test cases: 0, 1, -1, 0.5, -0.5

Avoid statement carryover - forget information from first statement when assessing second.

If you see that the two statements are identical, cross off (A), (B), and (C)

If statement (1) gets cannibalized, cross off (A) and (C)

If statement (2) gets cannibalized, cross off (B) and (C)

\[(4^x)^3 = 16^{x-1}\] \[((2^2)^x)^3 = (2^4)^{x-1}\] \[2^{6x} = 2^{4x-4}\] \[6x = 4x-4 => x = -2\]

\[\sqrt{x} = \sqrt[2]{x^1} = x^{1/2}\]

\[\frac{1}{8}^{-\frac{4}{3}} = 8^{\frac{4}{3}}=\sqrt[3]{8^4} = (\sqrt[3]{8})^4\]

\[\sqrt[4]{\sqrt{x}}=\sqrt[4]{x^\frac{1}{2}}=(x^\frac{1}{2})^{\frac{1}{4}}=x^\frac{1}{8}=\sqrt[8]{x}\]

\[\sqrt{68}=\sqrt{2\times2\times17}=\sqrt{4\times17}=\sqrt{4}\times\sqrt{17}=2\sqrt{17}\]

\[\sqrt{27}=\sqrt{3\times3\times3}=\sqrt{9\times3}=\sqrt{9}\times\sqrt{3}=3\sqrt{3}\]

\[\sqrt{\frac{68}{27}} = \frac{\sqrt{68}}{\sqrt{27}} = \frac{2\sqrt{17}}{3\sqrt{3}}\]

Splitting doesn’t work for addition, subtraction.

1.4² ≈ 2

1.7² ≈ 3

11² = 121

12² = 144

13² = 169

14² = 196

15² = 225

16² = 256

25² = 625

Beware disguised quadratics:

\[3x^2=6x\rightarrow x=?\]

Incorrect:

\[x^2=2x\\x=2\]

Correct:

\[3x^2-6x=0\\x^2-2x=0\\x(x-2)=0 \\x=0\hspace{0.3em}or\hspace{0.3em}2\]

\[x^2-y^2=(x+y)(x-y)\]

\[x^2+2xy+y^2=(x+y)(x+y)\]

\[x^2-2xy+y^2=(x-y)(x-y)\]

Can + - × / equality by value BUT if × or / by -ve, flip sign.

Can + BUT add 2× one:

\[a<c\\b<d\\a+2b<c+2d\]

Can × inequalities if all possible values are positive but cannot - or / inequalities.

\[x^2<4 \rightarrow x<2 | x > -2\]

A to B at 4kph.

B to A at 6kph.

Average speed?

NOT 5mph.

Pick smart number for distance e.g. common multiple → 12km.

A to B takes 3 hours. B to A takes 2 hours. Total = 24km in 5 hours → 4.8kph.

Total = 50.

31 in A.

24 in B.

13 in A and B.

How many in neither?

A Not A Total
B 13 11 24
Not B 18 8 26
Total 31 19 50

Can use Venn diagrams (overlapping circles) but the double-set matrix is better if only two sets of data points.

70% books are paperback.

Half hardback are fiction.

80% paperback are fiction.

Percent nonfiction? 29, 30, 50, 70, 71

For percentages, choose a total of 100.

For fractions, choose a common denominator.

PB HB Total
F 0.8T_PB = 56 0.5T_HB = 15 71
NF 70 - 56 = 14 30 - 15 = 15 29
Total 70 100-70 = 30 100

Beware evil twins e.g. 71 (% F, not NF)

Exam 1, 60% weighting, score 90

Exam 2, 40% weighting, score 70

Total score?

Approximate: Closer to 90 than 70 → >70

Algebraic:

\[90\times0.6+70\times0.4=82\]

or Teeter-Totter:

\[70+0.6(90-70)=82\]

\[90-0.4(90-70)=82\]

How many multiples of 6 between 10 and 80?

First = 12

Last = 78

\[\frac{78-12}{6}+1=12\]

What is the sum of all the integers from 13 to 47, inclusive?

\[\frac{13+47}{2}=25\\47-13+1=35\\25\times35=875\]

Hint: If given options, 5\times5 ends with 5, so answer must end in 5.

An integer is divisible by:

  • 3 if the sum of the integer’s digits is divisible by 3
  • 9 if the sum of the integer’s digits is divisible by 9
  • 4 if the integer is divisible by 2 twice or if the last two digits are divisible by 4
  • 8 if the integer is divisible by 2 three times or if the last three digits are divisible by 8

Fewer factors, more multiples

If you add or subtract multiples of N, the result is a multiple of N.

Dividend = Quotient × Divisor + Remainder (or, Dividend = Multiple of Divisor + Remainder)

If a is a factor of b, and b is a factor of c, then a is a factor of c.

The first ten prime numbers: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29.

Prime factors:

\[72=6\times12\\\rightarrow6=2\times3\\\rightarrow12=2\times2\times3\\72=2\times2\times2\times3\times3\]

Are 24 or 27 factors of 144?

Prime factors of 144: 2,2,2,2,3,3 (A)

Prime factors of 24: 2,2,2,3 (B)

Prime factors of 27: 3,3,3 (C)

All B in A → 24 is a factor of 144

All C not in A → 27 is not

If the integer x is divisible by 8 and 15, is x divisible by 12?

PF of 8: 2,2,2

PF of 15: 3,5

PF of x: 2,2,2,3,5 (at minimum) (A)

PF of 12: 2,2,3 (B)

All B in A → Yes

If the integer y is divisible by 8 and 10, is y divisible by 12?

PF of 8: 2,2,2

PF of 10: 2,5

PF of y: 2,2,2,5 (at minimum) → NOTE removed overlapping factor of 2

All B not in A → Maybe (e.g. 80 no vs 120 yes)

A OR B: P(A) + P(B)

A AND B: P(A) × P(B)

Seven people enter a race. The winner gets a platinum medal, the runner-up gets a gold medal, the next two each get a silver medal, and the rest get bronze medals. What is the number of different ways the medals can be awarded?

Runner 1 2 3 4 5 6 7
Medal P G S S B B B

\[\frac{7!}{1!1!2!3!}=\frac{7\times6\times5\times4\times3\times2\times1}{1\times1\times2\times1\times3\times2\times1}=7\times6\times5\times2\times1=420\]

A club must choose a delegation of 3 senior members and 2 junior members for an annual conference. If the club has 6 senior members and 5 junior members, how many different delegations are possible?

Seniors: 6 total, 3 yes →3 no

Junior: 5 total, 2 yes → 3 no

\[\frac{6!}{3!3!}\times\frac{5!}{2!3!}=20\times10=200\]

Two six-sided dice are rolled. What is the probability that the sum of the rolls is 8?

Denominator: 6 × 6 = 36

Numerator: 2+6, 3+5, 4+4, 5+3, 6+2 = 5

P = 5/36

If “at least” or “at most”, 1 − x shortcut:

A bag contains equal numbers of red, green, and yellow marbles. If James takes three marbles out of the bag, replacing each marble after picking it, what is the probability that at least one will be red?

\[P(≥1\hspace{0.3em}red)=1-P(0\hspace{0.3em}red)=1-(\frac{2}{3}\times\frac{2}{3}\times\frac{2}{3})=\frac{19}{27}\]

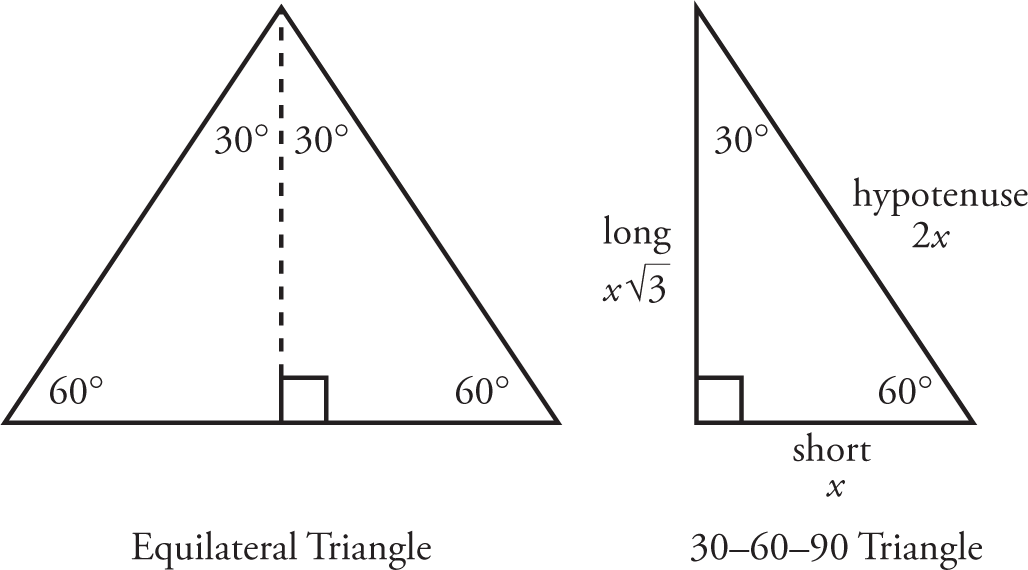
Triangles:

  • The sum of any two sides must be greater than the third side.
  • Any side must be greater than the difference between the lengths of the other two sides.
  • The length of a side must lie between the difference and the sum of the two other sides.

/img/gmat-quant-triangle-45.png

Note also half a square.

/img/gmat-quant-triangle-60.png

Note also half a rectangle.

/img/gmat-quant-circle.png

/img/gmat-quant-quadrants.png

Updated on 2023-01-14
 Maths, GMAT
Back | Home